МАШ 26. јун 2024. - група АМАШ 26. јун 2024. - група БМАШ 26. јун 2024. - група ЦМАШ 25. јун 2023. - група АМАШ 25. јун 2023. - група БМАШ 25. јун 2023. - група ЦМАШ 30. јун 2022. - група АМАШ 30. јун 2022. - група БМАШ 30. јун 2022. - група ЦМАШ 27. јун 2021. - група АМАШ 27. јун 2021. - група БМАШ 27. јун 2021. - група ЦМАШ 01. јул 2020. - група АМАШ 01. јул 2020. - група БМАШ 25. јун 2019. - група АМАШ 25. јун 2019. - група БМАШ 25. јун 2019. - група ЦМАШ 22. јун 2018. - група АМАШ 22. јун 2018. - група БМАШ 26. јун 2017. - група АМАШ 26. јун 2017. - група БМАШ 02. јул 2016. - група АМАШ 02. јул 2016. - група Б
Машински факултет, Београд. Пријемни испит - 25. јун 2019.
Укупан број поена који се може освојити на тесту је 60. Сваки тачан одговор доноси 3 поена. Изабрана опција "Н" (не знам) доноси нула поена, док сваки погрешан одговор доноси негативне поене (по -0,3 поена). Taкође, ако не изаберете ниједан од понуђених одговора ("А-Д" или "Н") добијате негативне поене.
1.
Вредност израза [inline]\dfrac{2x^2+7x+3}{x^3-1}-\dfrac{1-2x}{x^2+x+1}-\dfrac{3}{x-1}[/inline] за [inline]x=-\dfrac{1}{3}[/inline] је:A) [inline]\displaystyle-\frac{3}{2}[/inline];B) [inline]\displaystyle-\frac{3}{4}[/inline];C) [inline]\displaystyle\frac{3}{4}[/inline];D) [inline]\displaystyle\frac{4}{3}[/inline];E) [inline]\displaystyle-\frac{4}{3}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
2.
Вредност израза [inline]\sqrt[3]{20+14\sqrt2}+\sqrt[3]{20-14\sqrt2}[/inline] је:A) [inline]4[/inline];B) [inline]3[/inline];C) [inline]2[/inline];D) [inline]8\sqrt[3]5[/inline];E) [inline]2\sqrt[3]5[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
3.
Скуп свих реалних решења неједначине [inline]|x+2|+|x-2|\leq12[/inline] је:A) [inline][-8,4][/inline];B) [inline][-4,8][/inline];C) [inline][-3,2][/inline];D) [inline][-6,6][/inline];E) [inline][-6,2][/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
4.
Скуп решења неједначине [inline]\dfrac{x^2-2}{x^2-x-2}\geq\dfrac{1}{2}[/inline] је:A) [inline](-\infty,-2]\cup[1,+\infty)[/inline];B) [inline](-\infty,-2)\cup(-1,1)\cup(2,+\infty)[/inline];C) [inline](-\infty,-2]\cup(-1,1]\cup[2,+\infty)[/inline];D) [inline](-\infty,-2]\cup(2,+\infty)[/inline];E) [inline](-\infty,-2]\cup(-1,1]\cup(2,+\infty)[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
5.
Ако је полином [inline]x^3+2x^2+ax+b[/inline] дељив полиномом [inline]x^2+x+ab(a.b\in\mathbb{R})[/inline], онда је [inline]a
+b[/inline] једнако:A) [inline]1[/inline];B) [inline]\dfrac{1}{3}[/inline];C) [inline]-1[/inline];D) [inline]3[/inline];E) [inline]-3[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
6.
Колико реалних решења има једначина [inline]\sqrt x+\sqrt[4]x=0,3[/inline]?A) [inline]1[/inline];B) [inline]0[/inline];C) [inline]2[/inline];D) [inline]3[/inline];E) [inline]4[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
7.
Колико износи збир решења једначине [inline]3^{2x}-7\cdot3^{x-1}+1=0[/inline]?A) [inline]-1[/inline];B) [inline]0[/inline];C) [inline]1[/inline];D) [inline]\dfrac{10}{3}[/inline];E) [inline]\dfrac{10}{9}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
8.
Ако је [inline]\log_37=a[/inline] и [inline]\log_32=b[/inline], онда је [inline](\log_27+\log_72)^{-1}[/inline] једнако:A) [inline]\displaystyle\frac{a^2-b^2}{ab}[/inline];B) [inline]\displaystyle\frac{a^2+b^2}{ab}[/inline];C) [inline]\displaystyle\frac{ab}{a^2+b^2}[/inline];D) [inline]\displaystyle\frac{2a+7b}{3ab}[/inline];E) [inline]\displaystyle\frac{7a+2b}{ab}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
9.
Вредност израза [inline]\left(\dfrac{1+i\sqrt7}{2}\right)^4+\left(\dfrac{1-i\sqrt7}{2}\right)^4[/inline] је:A) [inline]4[/inline];B) [inline]2[/inline];C) [inline]1[/inline];D) [inline]0[/inline];E) [inline]-3\sqrt7i[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
10.
Комплексни број [inline]z[/inline] има својство да је [inline]\operatorname{Re} z[/inline] три пута веће од [inline]\operatorname{Im} z[/inline]. Колико је пута [inline]\operatorname{Re} (z^2)[/inline] веће од [inline]\operatorname{Im} (z^)[/inline]?A) [inline]\displaystyle\frac{8}{3}[/inline];B) [inline]\displaystyle\frac{4}{3}[/inline];C) [inline]\displaystyle\frac{10}{3}[/inline];D) [inline]\displaystyle\frac{5}{3}[/inline];E) [inline]9[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
11.
Ако је [inline]0< x<\dfrac{\pi}{2}[/inline] и [inline]\tg2x=-\dfrac{1}{3}[/inline], онда је [inline]\tg x[/inline] једнако:A) [inline]3+\sqrt{10}[/inline];B) [inline]\sqrt{10}-3[/inline];C) [inline]3+\sqrt{8}[/inline];D) [inline]3-\sqrt{8}[/inline];E) [inline]-\dfrac{1}{6}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
12.
Број решења једначине [inline]\sin^3x\cos x-\sin x \cos^3x=\dfrac{1}{8}[/inline] у интервалу [inline][0,2\pi)[/inline] је:A) [inline]0[/inline];B) [inline]2[/inline];C) [inline]4[/inline];D) [inline]6[/inline];E) [inline]8[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
13.
Обим правоугаоника је [inline]14[/inline], а његова површина [inline]10[/inline]. Тангенс оштрог угла између дијагонала правоугаоника је:A) [inline]\displaystyle\frac{20}{29}[/inline];B) [inline]\displaystyle\frac{20}{21}[/inline];C) [inline]\displaystyle\frac{4}{5}[/inline];D) [inline]\displaystyle\frac{29}{20}[/inline];E) [inline]\displaystyle\frac{21}{20}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
14.
Основа пирамиде је квадрат странице [inline]2\sqrt3\text{ cm}[/inline], а висина пирамиде је [inline]3\text{ cm}[/inline] и она садржи средиште једне од ивице основе. Полупречник сфере описане око ове пирамиде је:A) [inline]3\text{ cm}[/inline];B) [inline]2\sqrt3\text{ cm}[/inline];C) [inline]\sqrt7\text{ cm}[/inline];D) [inline]4\sqrt2\text{ cm}[/inline];E) [inline]\dfrac{3}{2}\sqrt5\text{ cm}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
15.
Када се омотач купе развије у равни, добија се четвртина круга полупречника [inline]4\sqrt5[/inline]. запремина те купе једнака је:A) [inline]\displaystyle\frac{100\pi}{\sqrt3}[/inline];B) [inline]\displaystyle\frac{25\pi\sqrt2}{3}[/inline];C) [inline]\displaystyle\frac{20\pi\sqrt5}{3}[/inline];D) [inline]\displaystyle\frac{25\pi\sqrt3}{3}[/inline];E) [inline]\displaystyle\frac{50\pi\sqrt3}{3}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
16.
Полупречник кружнице са центром [inline]C(2,5)[/inline] која споља додирује кружницу [inline](x+2)^2+(y-1)^2=2[/inline] је:A) [inline]4[/inline];B) [inline]2[/inline];C) [inline]3\sqrt2[/inline];D) [inline]4\sqrt2-2[/inline];E) [inline]4-\sqrt2[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
17.
Три броја чија је сума [inline]93[/inline] представљају узастопне чланове геометријске прогресије. Иста та три броја представљају први, други и седми члан аритметичке прогресије. Производ та три броја је:A) [inline]3175[/inline];B) [inline]3275[/inline];C) [inline]3375[/inline];D) [inline]3475[/inline];E) [inline]3575[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
18.
Збир биномних коефицијената трећег члана од почетка и трећег члана од краја у развоју израза [inline](\sqrt[4]3+\sqrt[3]4)^n(n\in\mathbb{N})[/inline] једнак је [inline]2450[/inline]. Број рационалних чланова у том развоју је:A) [inline]0[/inline];B) [inline]2[/inline];C) [inline]4[/inline];D) [inline]6[/inline];E) [inline]8[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
19.
Ако график функције [inline]f(x)=\dfrac{1}{x^2-mx+2}[/inline] садржи тачку [inline]M\left(-3,\dfrac{1}{19}\right)[/inline], онда је највећа вредност ове функције једнака:A) [inline]\displaystyle\frac{4}{3}[/inline];B) [inline]\displaystyle\frac{3}{4}[/inline];C) [inline]\displaystyle\frac{9}{2}[/inline];D) [inline]\displaystyle\frac{2}{9}[/inline];E) [inline]\displaystyle\frac{8}{3}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
20.
На слици је приказан график функције: 
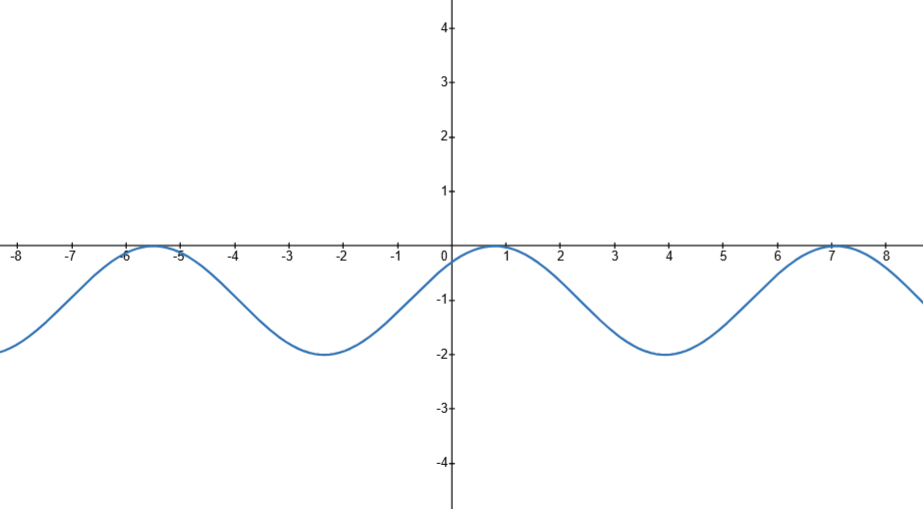
A) [inline]\sin\left(x-\dfrac{\pi}{4}\right)-1[/inline];B) [inline]\sin\left(x-\dfrac{\pi}{4}\right)+1[/inline];C) [inline]\sin\left(x-\dfrac{\pi}{4}\right)[/inline];D) [inline]\sin\left(x+\dfrac{\pi}{4}\right)+1[/inline];E) [inline]\sin\left(x+\dfrac{\pi}{4}\right)-1[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
