Електротехнички факултет, Београд. Пријемни испит - 29. јун 2020.

Вредност израза [inline]\log_43\log_54\log_65\log_76\log_87\log_98[/inline] једнака је:
A) [inline]\displaystyle\frac{1}{2}[/inline]B) [inline]\displaystyle\frac{1}{3}[/inline]C) [inline]2[/inline]D) [inline]3[/inline]E) [inline]\displaystyle\frac{2}{3}\log_23[/inline]N) Не знам

Ако је површина кружног исечка једнака [inline]15\%[/inline] површине круга, колики је угао тог кружног исечка?
A) [inline]15^\circ[/inline]B) [inline]30^\circ[/inline]C) [inline]45^\circ[/inline]D) [inline]54^\circ[/inline]E) [inline]60^\circ[/inline]N) Не знам

Вредност израза [inline]\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt6\right)\sqrt{4-\sqrt{15}}[/inline] једнака је:
A) [inline]\displaystyle\frac{1}{2}[/inline]B) [inline]1[/inline]C) [inline]2[/inline]D) [inline]\sqrt2[/inline]E) [inline]\displaystyle\frac{\sqrt2}{2}[/inline]N) Не знам

Инверзна функција функције [inline]f\colon[3,+\infty)\to[3,+\infty)[/inline] дате са [inline]f(x)=3\sqrt{x-3}+3[/inline] јесте функција [inline]g\colon[3,+\infty)\to[3,+\infty)[/inline] за коју важи:
A) [inline]\displaystyle g(x)=\frac{1}{9}x^2-\frac{2}{3}x+4[/inline]B) [inline]\displaystyle g(x)=\frac{1}{9}x^2+\frac{2}{3}x+4[/inline]C) [inline]\displaystyle g(x)=\frac{1}{9}x^2+\frac{2}{3}x-2[/inline]D) [inline]\displaystyle g(x)=\frac{1}{9}x^2-\frac{2}{3}x+2[/inline]E) [inline]\displaystyle g(x)=9\left(x^2-6x+\frac{28}{3}\right)[/inline]N) Не знам

График функције [inline]f(x)=ax^2+bx+c[/inline], [inline]a,b,c\in\mathbb{R}[/inline], [inline]x\in\mathbb{R}[/inline], дат је на слици.

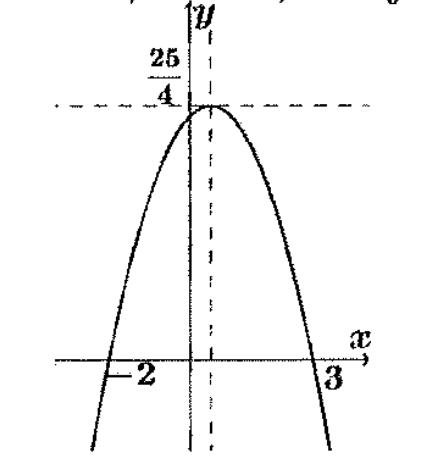
Вредност израза [inline]a(b+c)[/inline] једнака је:
A) [inline]-1[/inline]B) [inline]5[/inline]C) [inline]7[/inline]D) [inline]-7[/inline]E) [inline]6[/inline]N) Не знам

Производ најмањег и највећег корена полинома [inline]P(x)=x^4-9x^2+18[/inline] јесте:
A) [inline]3[/inline]B) [inline]-3[/inline]C) [inline]6[/inline]D) [inline]-6[/inline]E) [inline]-\sqrt{18}[/inline]N) Не знам

Реални део комплексног броја [inline]\left(z-z^2+2z^3\right)\left(2-z+z^2\right)[/inline], за [inline]\displaystyle z=\frac{-1+i\sqrt3}{2}[/inline], [inline]i^2=-1[/inline], једнак је:
A) [inline]4\left(1+\text{Im }^2z\right)[/inline]B) [inline]0[/inline]C) [inline]4[/inline]D) [inline]\displaystyle-\frac{1}{2}[/inline]E) [inline]-\text{Re }z+1[/inline]N) Не знам

Нека је дефинисан низ функција [inline]f_n\colon\mathbb{R}\to\mathbb{R}[/inline] са [inline]f_1(x)=2x+2020[/inline], [inline]f_{n+1}(x)=f_1\bigl(f_n(x)\bigr)[/inline], [inline]n\in\mathbb{N}[/inline]. Тада је [inline]f_{2020}(-2020)[/inline] једнако:
A) [inline]2^{2020}[/inline]B) [inline]-2^{2020}[/inline]C) [inline]2020[/inline]D) [inline]-2020[/inline]E) [inline]0[/inline]N) Не знам

Фигура [inline]F_1[/inline] добијена је тако што је из једнакостраничног троугла чија је површина [inline]P[/inline] избачен троугао чија су темена средишта страница полазног троугла. Фигура [inline]F_1[/inline] се састоји из [inline]3[/inline] троугла. Фигура [inline]F_2[/inline] добијена је тако што су из фигуре [inline]F_1[/inline] избачена три троугла чија су темена средишта страница три троугла који чине фигуру [inline]F_1[/inline]. Фигура [inline]F_2[/inline] се састоји из [inline]9[/inline] троуглова. Фигура [inline]F_{n+1}[/inline] добијена је тако што је из фигуре [inline]F_n[/inline] избачено [inline]3^n[/inline] троуглова чија су темена средишта страница [inline]3^n[/inline] троуглова који чине фигуру [inline]F_n[/inline]. Збир површина свих фигура [inline]F_n[/inline], [inline]n\in\mathbb{N}[/inline], добијених на описани начин, једнак је:
A) [inline]\displaystyle\frac{3}{4}P[/inline]B) [inline]\displaystyle\frac{4}{3}P[/inline]C) [inline]4P[/inline]D) [inline]3P[/inline]E) [inline]+\infty[/inline]N) Не знам

Број свих реалних решења једначине [inline]2x^2-6x+\sqrt{x^2-3x+6}+2=0[/inline] јесте:
A) [inline]2[/inline]B) [inline]1[/inline]C) [inline]3[/inline]D) [inline]4[/inline]E) Већи од [inline]4[/inline]N) Не знам

Реално решење једначине [inline]x+\log_{21}\left(3^x+1\right)=x\log_{21}7+\log_{21}756[/inline] припада интервалу:
A) [inline](-\infty,-21][/inline]B) [inline](-21,0][/inline]C) [inline](0,21)[/inline]D) [inline][21,42)[/inline]E) [inline][42,+\infty)[/inline]N) Не знам

Дужина странице квадрата [inline]ABCD[/inline] једнака је [inline]8\text{ cm}[/inline]. Кружница пролази кроз темена [inline]A[/inline] и [inline]D[/inline] и додирује страницу [inline]BC[/inline]. Површина круга који одређује та кружница јесте:
A) [inline]16\pi\text{ cm}^2[/inline]B) [inline]25\pi\text{ cm}^2[/inline]C) [inline]\displaystyle\frac{64}{25}\pi\text{ cm}^2[/inline]D) [inline]64\pi\text{ cm}^2[/inline]E) [inline]\displaystyle\frac{25}{64}\pi\text{ cm}^2[/inline]N) Не знам

Колико има целобројних решења неједначине [inline]\left(\sqrt{7+4\sqrt3}\right)^{\cos x}+\left(\sqrt{7-4\sqrt3}\right)^{\cos x}\le4[/inline] која припадају интервалу [inline]\left[-2\pi,\;\sqrt3+\sqrt5\right][/inline]?
A) [inline]3[/inline]B) [inline]4[/inline]C) [inline]11[/inline]D) [inline]10[/inline]E) бесконачно многоN) Не знам

Скуп решења неједначине [inline]12\text{ arctg }^2x+\pi\text{ arctg }x-\pi^2\le0[/inline] је облика (за неке реалне бројеве [inline]a[/inline] и [inline]b[/inline] такве да је [inline]-\infty\lt a\lt b\lt\infty[/inline]):
A) [inline](-\infty,a]\cup[b,+\infty)[/inline]B) [inline][a,b][/inline]C) [inline]\displaystyle\bigcup\limits_{k\in\mathbb{Z}}[a+2k\pi,\;b+2k\pi][/inline]D) [inline]\displaystyle\bigcup\limits_{k\in\mathbb{Z}}[a+k\pi,\;b+k\pi][/inline]E) [inline]\displaystyle\left(-\frac{\pi}{2},a\right]\cup\left[b,\frac{\pi}{2}\right)[/inline]N) Не знам

Број свих реалних решења једначине [inline]\displaystyle\sin^2x+\frac{1}{\sin^2x}=\sin x[/inline] јесте:
A) [inline]0[/inline]B) [inline]1[/inline]C) [inline]2[/inline]D) [inline]3[/inline]E) већи од [inline]3[/inline]N) Не знам

Ако су тачке [inline]M[/inline], [inline]N[/inline], [inline]P[/inline] и [inline]Q[/inline] средишта ивица [inline]DA[/inline], [inline]AB[/inline], [inline]BC[/inline] и [inline]CD[/inline] правилног тетраедра [inline]ABCD[/inline] ивице дужине [inline]a[/inline], онда је површина четвороугла [inline]MNPQ[/inline] једнака:
A) [inline]\displaystyle\frac{a^2}{4}[/inline]B) [inline]\displaystyle\frac{a^2\sqrt3}{4}[/inline]C) [inline]\displaystyle\frac{a^2\sqrt2}{2}[/inline]D) [inline]\displaystyle\frac{a^2}{2}[/inline]E) [inline]\displaystyle\frac{a^2\sqrt3}{3}[/inline]N) Не знам

Скуп решења једначине [inline]\displaystyle(\log_{\sin x}2)\left(\log_{\sin^2x}\frac{4}{3}\right)=2\log_\frac{4}{3}2[/inline] има тачно три заједничка елемента са скупом [inline]S[/inline], ако је:
A) [inline]\displaystyle S=\left\{\frac{\pi}{4},\frac{3\pi}{4},\frac{5\pi}{4},\frac{7\pi}{4},\frac{11\pi}{4},\frac{15\pi}{4}\right\}[/inline]B) [inline]\displaystyle S=\left\{\frac{\pi}{6},\frac{5\pi}{6},\frac{\pi}{3},\frac{2\pi}{3},\frac{7\pi}{6},\frac{11\pi}{6}\right\}[/inline]C) [inline]\displaystyle S=\left\{\frac{\pi}{3},\frac{2\pi}{3},-\frac{\pi}{3},-\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3}\right\}[/inline]D) [inline]\displaystyle S=\left\{\frac{\pi}{3},\frac{7\pi}{3},\frac{13\pi}{3},\frac{19\pi}{3},\frac{25\pi}{3},\frac{31\pi}{3}\right\}[/inline]E) [inline]\displaystyle S=\left\{\frac{2\pi}{3},-\frac{4\pi}{3},-\frac{5\pi}{3},-\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3}\right\}[/inline]N) Не знам

У тетивном четвороуглу [inline]ABCD[/inline] дијагонала [inline]BD[/inline] је нормална на страницу [inline]BC[/inline], углови [inline]\angle ABC[/inline] и [inline]\angle BAD[/inline] су једнаки [inline]120^\circ[/inline], а дужина странице [inline]AD[/inline] јесте [inline]1\text{ cm}[/inline]. Производ дужине дијагонале [inline]BD[/inline] и дужине странице [inline]CD[/inline] једнак је:
A) [inline]\displaystyle\frac{\sqrt3}{2}\text{ cm}^2[/inline]B) [inline]\sqrt3\text{ cm}^2[/inline]C) [inline]2\sqrt3\text{ cm}^2[/inline]D) [inline]6\sqrt3\text{ cm}^2[/inline]E) [inline]2\text{ cm}^2[/inline]N) Не знам

Дате су тачке [inline]A(2,2)[/inline], [inline]A'(-2,-2)[/inline], [inline]B(4,-4)[/inline] и [inline]B'(-4,4)[/inline]. Дужи [inline]AA'[/inline] и [inline]BB'[/inline] су осе елипсе [inline]\varepsilon[/inline]. Ако је [inline]Y(0,y_0)[/inline], [inline]y_0>0[/inline], тачка пресека [inline]y[/inline]-осе и елипсе [inline]\varepsilon[/inline], онда је [inline]y_0[/inline] једнако:
A) [inline]\displaystyle\frac{8}{\sqrt5}[/inline]B) [inline]\displaystyle\frac{4\sqrt2}{\sqrt5}[/inline]C) [inline]\displaystyle\frac{8\sqrt2}{\sqrt5}[/inline]D) [inline]\displaystyle\frac{4}{\sqrt5}[/inline]E) [inline]\displaystyle\frac{32}{\sqrt5}[/inline]N) Не знам

Вредност израза [inline]\text{tg }10^\circ-\text{tg }50^\circ+\text{tg }70^\circ[/inline] јесте:
A) [inline]\displaystyle\frac{\sqrt3}{3}[/inline]B) [inline]3\sqrt3[/inline]C) [inline]3[/inline]D) [inline]-1[/inline]E) [inline]\sqrt3[/inline]N) Не знам