МАТФ 18. јун 2024. - ПробниМАТФ 28. јун 2023.МАТФ 17. јун 2023. - ПробниМАТФ 29. јун 2022.МАТФ 11. јун 2022. - ПробниМАТФ 30. јун 2021.МАТФ 12. јун 2021. - ПробниМАТФ 01. јул 2020.МАТФ 26. јун 2019.МАТФ 15. јун 2019. - ПробниМАТФ 27. јун 2018.МАТФ 16. јун 2018. - ПробниМАТФ 28. јун 2017.МАТФ 10. јун 2017. - ПробниМАТФ 29. јун 2016.МАТФ 29. јун 2015.МАТФ 09. јул 2014.МАТФ 14. јун 2014. - ПробниМАТФ 02. јул 2013.
Математички факултет, Београд. Пријемни испит - 29. јун 2015.
Тест има 20 задатака на 2 странице. Сви задатци се вреднују са по 5 поена. Уколико не желите да се определите за један од првих пет понуђених одговора можете да означите „Н“, што се вреднује са 0 поена. За погрешан одговор се одузима 0.5 поена. Ако се, за конкретан задатак, означи више од једног или не означи ниједан одговор, као и ако се на било који начин неправилно означи одговор, одузима се 1 поен.
1.
Подножје висине дели хипотенузу правоуглог троугла на одсечке чије су дужине [inline]16\text{ cm}[/inline] и [inline]9\text{ cm}[/inline]. Полупречник круга уписаног у тај троугао је:A) [inline]4\text{ cm}[/inline];B) [inline]5\text{ cm}[/inline];C) [inline]6\text{ cm}[/inline];D) [inline]8\text{ cm}[/inline];E) [inline]10\text{ cm}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
2.
Ако је ивица коцке једнака [inline]a[/inline], полупречник сфере која додирује свих дванаест ивица те коцке једнак је:A) [inline]a[/inline];B) [inline]a\sqrt2[/inline];C) [inline]\displaystyle\frac{a\sqrt2}{2}[/inline];D) [inline]a\sqrt3[/inline];E) [inline]\displaystyle\frac{a\sqrt3}{2}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
3.
Дате су кружна линија [inline]k[/inline] једначином [inline]x^2+y^2=a^2[/inline], [inline]a>0[/inline], и тачка [inline]P\left(a,a\right)[/inline]. Нека су [inline]A[/inline] и [inline]B[/inline] тачке у којима права [inline]PO[/inline] сече [inline]k[/inline], где је [inline]O[/inline] координатни почетак. Производ [inline]PA\cdot PB[/inline] једнак је:A) [inline]\displaystyle\frac{a^2}{2}[/inline];B) [inline]a^2[/inline];C) [inline]2a^2[/inline];D) [inline]a^2\sqrt2[/inline];E) [inline]\displaystyle\frac{a^2}{\sqrt2}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
4.
Ако је однос углова неког троугла једнак [inline]3:4:5[/inline], онда је однос његових страница једнак:A) [inline]2:\sqrt6:\left(1+\sqrt3\right)[/inline];B) [inline]\sqrt3:\sqrt4:\sqrt5[/inline];C) [inline]\left(1+\sqrt2\right):\sqrt6:\left(1+\sqrt3\right)[/inline];D) [inline]3:4:5[/inline];E) [inline]\displaystyle\frac{1}{3}:\frac{1}{4}:\frac{1}{5}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
5.
Најмањи реалан број [inline]a[/inline] за који једначина [inline]\cos^4x+\sin^4x=a[/inline] има решење једнак је:A) [inline]2[/inline];B) [inline]\sqrt2[/inline];C) [inline]1[/inline];D) [inline]\displaystyle\frac{1}{\sqrt2}[/inline];E) [inline]\displaystyle\frac{1}{2}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
6.
Периодични децимални број [inline]2,727272\ldots[/inline], чији се период састоји од две цифре, написан је у облику нескративог разломка. Збир бројиоца и имениоца тог разломка једнак је:A) [inline]369[/inline];B) [inline]299[/inline];C) [inline]123[/inline];D) [inline]41[/inline];E) [inline]29[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
7.
Скуп вредности параметра [inline]m[/inline] за које једначина [inline]\left(m-2\right)x^2-2mx+2m+2=0[/inline] има два реална решења супротног знака је:A) [inline]\left(-1,2\right)[/inline];B) [inline]\left(-2,1\right)[/inline];C) [inline]\left(-2,0\right][/inline];D) [inline]\left(0,2\right][/inline];E) [inline]\left[-1,1\right][/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
8.
Збир квадрата решења једначине [inline]\displaystyle x-\frac{2}{x}=i[/inline] једнак је:A) [inline]0[/inline];B) [inline]2i[/inline];C) [inline]5[/inline];D) [inline]-i[/inline];E) [inline]3[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
9.
На слици је дат график функције [inline]f\left(x\right)=ax^2+bx+c[/inline].
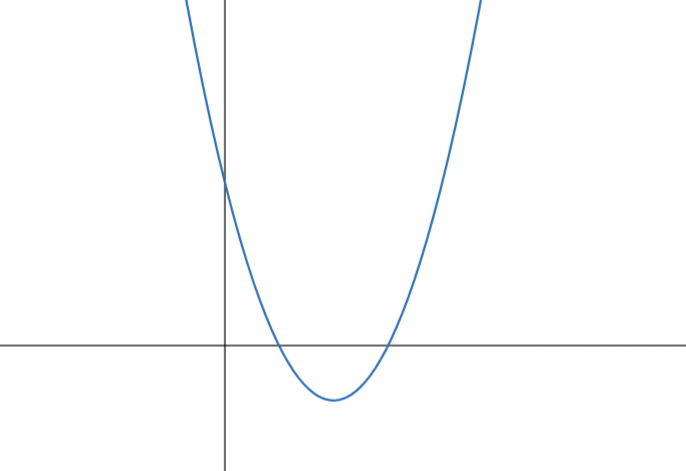
Колико има позитивних међу бројевима [inline]a[/inline], [inline]b[/inline], [inline]c[/inline], [inline]2ac-b^2[/inline] и [inline]a-b+c[/inline]?
A) [inline]1[/inline];B) [inline]2[/inline];C) [inline]3[/inline];D) [inline]4[/inline];E) [inline]5[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
10.
Полином [inline]x^{2015}+x^{2014}+ax+b[/inline] је дељив полиномом [inline]x^2-1[/inline]. Колико је [inline]a^2+b^2[/inline]?A) [inline]0[/inline];B) [inline]1[/inline];C) [inline]2[/inline];D) [inline]3[/inline];E) [inline]4[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
11.
Функција [inline]f\colon\mathbb{R}\to\mathbb{R}[/inline] задата је са [inline]f\left(x\right)=\left|x+1\right|+\left|2x+4\right|+4x[/inline]. Вредност израза [inline]f^{-1}\left(-7\right)+f^{-1}\left(-2\right)+f^{-1}\left(5\right)[/inline] је:A) [inline]-4[/inline];B) [inline]-3[/inline];C) [inline]0[/inline];D) [inline]4[/inline];E) [inline]14[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
12.
Операција [inline]\ast[/inline] је дефинисана на скупу позитивних реалних бројева са [inline]x\ast y=\sqrt{xy}[/inline]. Колико је [inline]\left(3\ast48\right)\ast9[/inline]?A) [inline]6\sqrt3[/inline];B) [inline]6\sqrt[4]3[/inline];C) [inline]6[/inline];D) [inline]36[/inline];E) [inline]108[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
13.
Функција [inline]f\colon\left(0,+\infty\right)\to\mathbb{R}[/inline] дефинисана је са [inline]f\left(x\right)=\log_6x+3\log_3\left(9x\right)[/inline]. Колико је [inline]\displaystyle f\left(x\right)+f\left(\frac{1}{x}\right)[/inline]?A) [inline]-2[/inline];B) [inline]9[/inline];C) [inline]12[/inline];D) [inline]15[/inline];E) [inline]27[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
14.
Скуп решења неједначине [inline]3\cdot4^x-5\cdot2^{x+1}\le8[/inline] је:A) [inline]\left(-\infty,2\right][/inline];B) [inline]\left[0,2\right][/inline];C) [inline]\displaystyle\left[-\frac{2}{3},4\right][/inline];D) [inline]\left[2,+\infty\right)[/inline];E) [inline]\left(3,8\right)[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
15.
Ако је [inline]-1<x<0[/inline], који је број највећи:A) [inline]\displaystyle\frac{3}{x^2}[/inline];B) [inline]3^{1/x}[/inline];C) [inline]\displaystyle\frac{-3}{x}[/inline];D) [inline]3^x[/inline];E) [inline]\displaystyle\frac{3}{\sqrt{-x}}[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
16.
Низ [inline]\left(a_n\right)[/inline] је задат са [inline]a_1=1[/inline], [inline]a_{2n}=a_n-1[/inline], [inline]a_{2n+1}=a_n+1[/inline]. Колико је [inline]a_{2015}[/inline]?A) [inline]5[/inline];B) [inline]0[/inline];C) [inline]8[/inline];D) [inline]9[/inline];E) [inline]10[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
17.
Дата је аритметичка прогресија [inline]a_1,a_2,a_3,\ldots[/inline]. Ако је [inline]a_1=3[/inline], [inline]a_n=136[/inline] и [inline]\displaystyle\sum_{k=1}^na_k=1390[/inline], колико је [inline]a_2[/inline]?A) [inline]6[/inline];B) [inline]13[/inline];C) [inline]8[/inline];D) [inline]20[/inline];E) [inline]10[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
18.
Коефицијент уз [inline]x^7[/inline] у развоју [inline]\displaystyle\left(\frac{x^2}{2}-\frac{2}{x}\right)^8[/inline] једнак је:A) [inline]\displaystyle\frac{7}{4}[/inline];B) [inline]-14[/inline];C) [inline]70[/inline];D) [inline]-224[/inline];E) [inline]448[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
19.
Број бијекција скупа [inline]\left\{1,2,3,4,5,6,7\right\}[/inline] у себе, које пресликавају парне бројеве у парне бројеве, једнак је:A) [inline]12[/inline];B) [inline]24[/inline];C) [inline]256[/inline];D) [inline]144[/inline];E) [inline]121[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
20.
Странице књиге су нумерисане природним бројевима [inline]1,2,3,\ldots[/inline] у децималном запису. Колико страница има књига, ако је за њихову нумерацију употребљено [inline]1500[/inline] цифара?A) [inline]500[/inline];B) [inline]512[/inline];C) [inline]536[/inline];D) [inline]550[/inline];E) [inline]555[/inline];N) Не знам
ПРИКАЗАТИ РЕШЕЊЕ
ПРИКАЗАТИ ПОСТУПАК
ПРИКАЗАТИ КОМЕНТАРЕ
ПИТАЊА И КОМЕНТАРИ
Овај задатак нема коментара.
*Морате бити логовани да бисте оставили коментар.
